Volume is the quantification of the three-dimensional space a substance occupies. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method.
Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. The cone height formula helps in calculating the distance from the vertex of the cone to the cone's base. The height of the cone can be calculated using either the volume of cube and radius or with slant height and radius of the cone. We can also define the cone as a pyramid with a circular cross-section, unlike a pyramid that has a triangular cross-section. Let us study the cone height formula using solved examples at the end of the page.
If a cone and cylinder have the same height and base radius, then the volume of cone is equal to one third of that of cylinder. That is, you would need the contents of three cones to fill up this cylinder. The same relationship holds for the volume of a pyramid and that of a prism . Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids.
If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere . Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly. In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections.
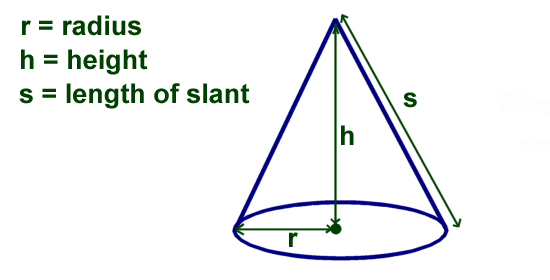
If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the lateral surface; if the lateral surface is unbounded, it is a conical surface. The radius of the cone is the length from the center of the circular base to the outside perimeter of the base.
The height is the length from the center of the circular base to the apex and runs inside the cone. The slant height is the length from the outside perimeter of the circular base to the apex, and it runs at an angle to the height. If looking at a cone in three dimensions, the height, radius, and slant height will form a right triangle, as depicted in the graphic below. A cone is a three dimensional geometric shape with one vertex and a circular base. The line form the centre of the base to the apex is the perpendicular height. A simple check on any formula for area or volume is a dimensional check.
Area is the two-dimensional amount of space that an object occupies. Area is measured along the surface of an object and has dimensions of length squared; for example, square feet of material, or square centimeters. Volume is the three-dimensional amount of space that an object occupies. Volume has dimensions of length cubed; for example, cubic feet of material, or cubic centimeters (cc's). First, take the measurement of the diameter , then measure or estimate the height.
If you already have plans or schematics, just get the lengths from there. Convert the length units to the same base, e.g. inches or centimeters, then follow the formula above or use our online volume of a cone calculator. The output is always in cubic units, e.g. cubic inches, cubic feet, cubic yards, cubic mm, cubic cm, cubic meters, and so on. Let's get right to it — we're here to calculate the surface area or volume of a right circular cone. As you might already know, in a right circular cone, the height goes from the cone's vertex through the center of the circular base to form a right angle.
Right circular cones are what we typically think of when we think of cones. In our everyday life, we come across different types of cones. The volume of cone formula can be used in manufacturing and calculating the capacity or volume of traffic cones, ice-cream cones, funnels and even the regular cylinders.
You can easily find out the volume of a cone if you have the measurements of its height and radius. In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top. In simple words, a cone is a pyramid with a circular base.
One can calculate theweightof any object by multiplying thedensityof the material by the volume of the object. On this slide, we list some equations for computing the volume of objects which often occur in aerospace. There are similar equations for computing theareaof objects. The magnitude of theaerodynamic forcesdepends on the surface area of an object, while thegravitational forceand certainthermodynamic effectsdepend on the volume of the object. The equations to compute area and volume are used every day by design engineers. In this example you need to calculate the volume of a very long, thin cylinder, that forms the inside of the pipe.
The area of one end can be calculated using the formula for the area of a circle πr2. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. Every cube, sphere, cylinder, cone , and so on has a volume and a surface area; and the formulas used for finding these measurements is different for each shape. The volume of a cone is easiest to find when the cone is standard in shape. A standard cone will have a base that is a circle in shape and the height will form a perfect right angle between the radius of the base and the apex.
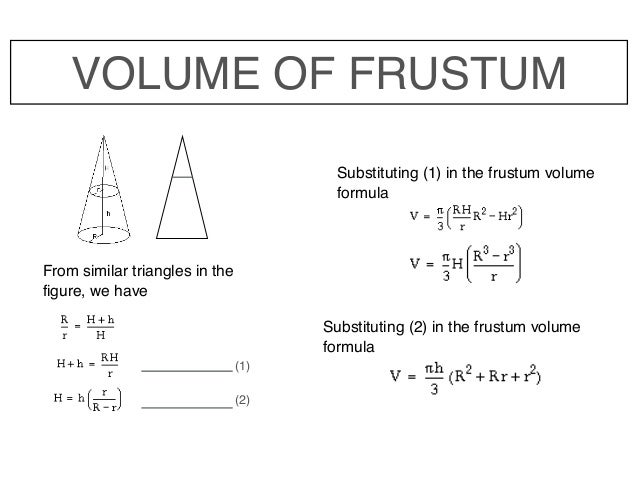
However, cones may also be irregularly shaped, which makes finding their volume slightly different. Oblique cones are those where the apex does not line up with the center of the base and thus the cone appears slanted. A frustrum appears like a normal cone with its tip cut off so that it has a flat base on one end and a flat top on the other. Below, explore how to find the volume of these unique shapes.
Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone. In geometry, a cone is a solid figure with one circular base and a vertex. The height of a cone is the distance between its base and the vertex.The cones that we will look at in this section will always have the height perpendicular to the base. With the Pythagorean theorem, use the radius and the height to calculate the slant height of the cone, then multiply the slant height by the radius by pi. To that you add the base area of the cone, which is found by multiplying pi by the square of the radius. The total surface area is found by adding the lateral surface area to the base area.
An oblique cone is a cone with an apex that is not aligned above the center of the base. It "leans" to one side, similarly to the oblique cylinder. The cone volume formula of the oblique cone is the same as for the right one. Since the cross sectional areas are also equal, we can employ Cavalieri's principle and state that the volume of the cone equals the volume of the pyramid.
Since the height is the same in both solids, B must equal πr2 for the cone, making the formula for the volume of a cone . Combined with scaling, this does it for all pyramids, hence also cones. The slant height of a cone should not be confused with the height of a cone.
Slant height is the distance from the top of a cone, down the side to the edge of the circular base. Slant height is calculated as \(\sqrt\), where \(r\) represents the radius of the circular base, and \(h\) represents the height, or altitude, of the cone. Finding the volume of an oblique cone is simple when identifying what the variables are. In fact, the equation for finding the volume remains the same as the standard cone described above. The only change is that the height is determined differently.
Recall that the height was found before by drawing a line from the apex to the center of the base that resulted in a right angle. In an oblique cone, the height is still found by drawing a straight line from the apex to the base, though the height will not end at the center. Instead, the height will end at the point that lines up with the base where a right angle is formed, even if it is outside of the cone itself. If you have the diameter, cut it in half to get the radius. If you have the slant height and perpendicular height, use the Pythagorean theorem. There is special formula for finding the volume of a cone.
The volume is how much space takes up the inside of a cone. The answer to a volume question is always in cubic units. In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height of a cone. A cone's slanted lines are the length of a cone along the taper curved surface. All of these parameters are mentioned in the figure above. A cone has a three-dimensional shape so calculating its volume can seem a little complicated.
To help you understand better, in this article we explain what a cone is as well as how to calculate its volume. We detail the steps one by one and the formulas you have to use to calculate the volume of a cone with accurate examples. The cone can be defined as the three dimensional object with a circular base.
The volume of the cone is measured in cubic units. Be sure that all of the measurements are in the same unit before computing the volume. A cone with a region including its apex cut off by a plane is called a "truncated cone"; if the truncation plane is parallel to the cone's base, it is called a frustum.
An "elliptical cone" is a cone with an elliptical base. A "generalized cone" is the surface created by the set of lines passing through a vertex and every point on a boundary . Thus we can derive a formula for the volume of a cone of any shaped base if we can do so for some one shaped base. We can conclude from this experiment that the volume of a cylinder is thrice the volume of a cone having the same height and base radius. This implies that the volume of a cone is equal to one-third of the volume of the cylinder having the same height and base radius. The volume of a cone is the amount of space a cone takes up in three dimensions.
This is different from the surface area, which is the total amount of two-dimensional space needed to completely wrap around the cone. Volume is given in cubic units, while surface area is given in square units. I then observed how the volume of the cone could be approximated by using disks, the width of each being the height of the cone divided by the number of disks. So, the volume as a function of x would be the area as a function of x times the height divided by n, or the number of disks. First, I put a cone on a Cartesian plane, with the tip at the origin.
Thus, an equation to describe the radius would be the radius over the height times x. Then, I substituted this equation into pi r squared to get cross sectional area as function of x. I just did a demonstration with my class that took about 2 minutes. Granted it was just inductive reasoning but it satisfied the students for now. I had 2 pairs of students come up to the front of the class. Each pair had solids with a congruent base and height.
The person with the cone had to see how many times they could fill the cone with water and fit it into the cylinder. Similarly the person with the pyramid had to see how many times they could fill the pyramid with water and fit it into the prism. A cone is a three-dimensional figure with one circular base. A curved surface connects the base and the vertex. In this method, you are basically calculating the volume of the cone as if it was a cylinder.
When you calculate the area of the base circle, and multiply it by the height, you are "stacking" the area up until it reaches the height, thus creating a cylinder. And because a cylinder can fit three cones of its matching measurements, you multiply it by one third so that it's the volume of a cone. And if you don't know any of the measurements of the shape, just use a ruler to measure the widest pie circular base and divide that number by 2 to get the radius. Let's say the radius of this cone's circular base is .5 inches (1.3 cm). We now have a formula for the volume of any square-based pyramid whose vertex is above one of the vertices of the base.
What about if the vertex is somewhere else - the middle, for instance? What we are going to do is to imagine the pyramid cut into lots of slices horizontally. We are going to slide these slices across, so that the top of the pyramid is above the middle of the base. When we think of a pyramid, we usually think of one where the vertex is above the centre of the base, a right pyramid . However in this article, we will begin with a yangma. Yangma is an ancient Chinese name for a rectangular-based pyramid whose vertex is vertically above one of the vertices of the base.
We will take a yangma with a square base of side length $a$, and height also length $a$. Three of these can be fitted together to form a cube. These formulae are often quoted, but rarely proved. In this article, we derive the formulae for the volumes of a square-based pyramid and a cone, using relatively simple mathematical concepts. Just as you can calculate the area of irregular two-dimensional shapes by breaking them down into regular ones, you can do the same to calculate the volume of irregular solids. Just split the solid up into smaller parts until you reach only polyhedrons that you can work with easily.
The "height" of a cone, and the "slant height" of a cone are not the same thing. The height of a cone is considered the vertical height or altitude of the cone. This is the perpendicular distance from the top of the cone down to the center of the circular base. The slant height of a cone is the distance from the top of the cone, down the side of the cone to the edge of the circular base. Welcome to today's video where we're going to talk about the volume and surface area of a cone.
We know that a cone is actually a lot like a pyramid. While a pyramid has a square base that connects to a pointy tip at the opposite end, a cone's base is, instead, a circle. Find the total surface area of a cone, whose base radius is 3 cm and the perpendicular height is 4 cm. Imagine a cone whose base is a circle radius $r$, and height is $h$. This will look like a square with a circle fitting inside. We don't know the radius of the cone at this point, so we'll call it $x$.















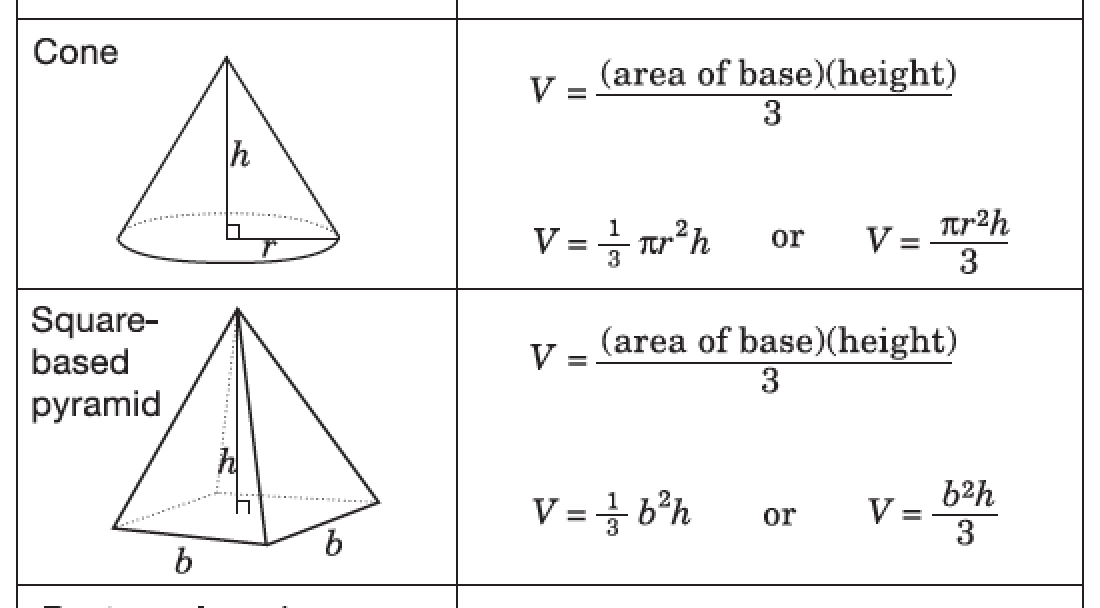








No comments:
Post a Comment
Note: Only a member of this blog may post a comment.